Capítulo 6 Análisis de los Datos
6.1 Análisis Univariante
Estudia la distribución individual de cada variable. Este análisis se centra en dos aspectos: La tendencia central de la distribución y su dispersión. En el primer caso hablamos de un valor característico o medio de la distribución, en el segundo de la variabilidad interna de los datos. Según el tipo de variables proceden los siguientes análisis:
- Variables nominales. Para este tipo de variables el análisis se limita a las frecuencias de cada categoría. Se suele expresar en porcentajes.
- Variables ordinales. La tendencia central se mide con los estadísticos mediana y moda (pero no la media, ya que ésta implica distancias comparables), mientras que para la dispersión podemos utilizar un diagrama de frecuencias (histograma).
- Variables métricas. Para el análisis de la tendencia central se utiliza por lo general la media, si bien es aconsejable utilizar la mediana cuando nos encontramos con unos pocos valores extremos cuya magnitud difiere ampliamente del resto (son mucho mayores o mucho menores que la mayoría). Para estudiar el grado de dispersión recurrimos a la desviación típica o la varianza. Es posible estudiar además del momento de primer orden de la distribución (tendencia central) y el momento de segundo orden (dispersión), el momento de tercer orden (simetría) y el de cuarto orden (achatamiento). No es frecuente estudiar momentos de orden superior.
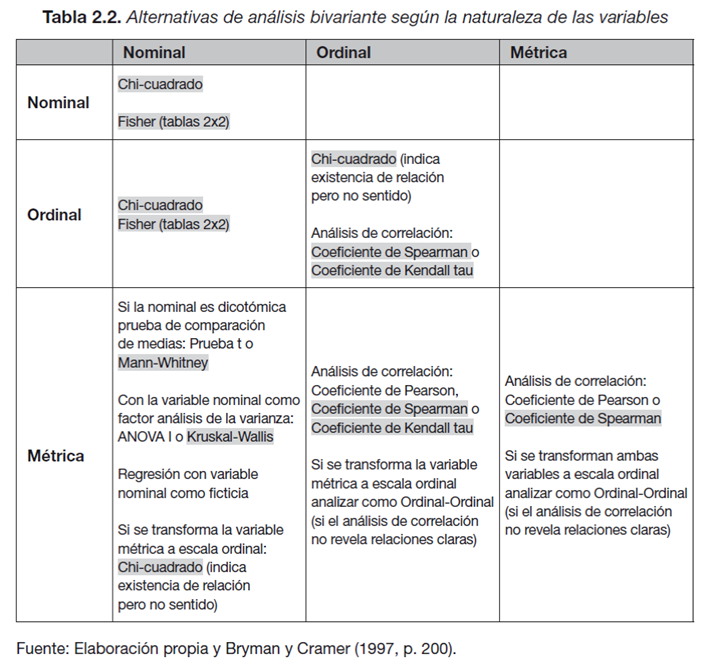
6.2 Análisis Vibariante
- Distribución normal de las variables.
- Para llevar a cabo pruebas de estadística paramétrica se asume que la variable estudiada de la población sigue una dsitribución normal.
- Uniformidad de la varianza.
- Se requiere que la varianza de una variable no dependa del nivel de otra variable.
- Escala de medida.
- Las variables deben medirse en una escala métrica.
- Independencia.
- Las respuestas de un sujeto no dependen de las de otro.
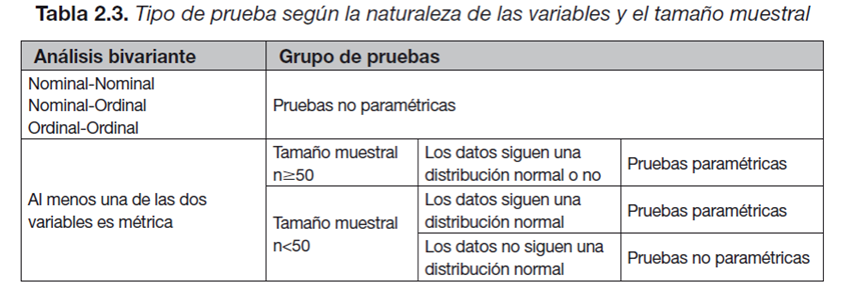
6.3 Análisis Multivariante
- Análisis de la varianza (ANOVA II). Se analiza el efecto de dos variables nominales (llamadas factores) sobre una variable métrica.
Ejemplo: ¿Depende el rendimiento de una máquina (variable métrica) del modelo de la máquina (factor 1) y del operario que la manjea (factor 2)?
- Análisis multivariante de la varianza (MANOVA). A diferencia de ANOVA, éste análisis considera simultáneamente dos o más variables dependeintes. En este caso, ¿por qué no utilizar ANOVA para cada una de las variables dependeintes? La respuesta es simple: porque es posible que exista una diferencia entre grupos que sólo se ponga en evidencia considerando varias variables dependientes simultáneamente.
- Análisis discriminante. La idea central de ésta técnica consiste en ponderar las diferentes variables a la hora de asignar un elemento a un grupo u otro. Por tanto, la variable dependiente es nominal mientras que las explicativas pueden ser de cualquier tipo.
Ejemplo: ¿Podríamos predecir el tipo de coche (variable nominal) que un consumidor compraría en función de su nivel de ingresos (variable ordinal), sexo (variable nominal) y edad (variable métrica)?
- Análisis de regresión lineal múltiple. Se estudia el efecto simultáneo de un conjunto de variables de cualquier tipo (variables explicativas) sobre una variable métrica (variable dependiente).
Ejemplo: ¿Cómo influye en el rendimiento de una máquina el modelo de la misma, el operario que la maneja, su antigüedad y el turno de trabajo?
6.4 Pruebas de Hipótesis
6.4.1 Generalidades
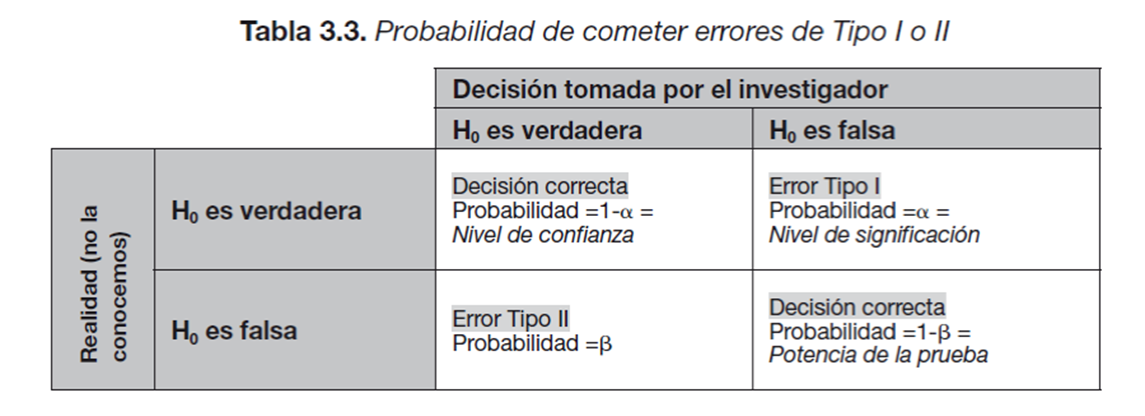
6.4.2 Errores Tipo I y Tipo II
6.4.3 Prueba de una cola
Queremos determinar si el tratamiento A contra una plaga reduce significativamente la incidencia de la misma sobre el cultivo. Para ello medimos el número de gusanos por planta en 5 parcelas con tratamiento y en 5 parcelas sin tratamiento. En este caso, lo lógico es pensar que el tratamiento no va a incrementar el número de gusanos y que, si tiene algún efecto, será reducir dicho número. Este es un caso de prueba de una cola. < br> La hipótesis se formula como sigue:
\[H_0: \mu_0 = \mu_A \text{ <--- (no existe diferencia entre las dos medias)}\]
\[H_A: \mu_0 > \mu_A \text{ <--- (la media de las fincas sin tratar es mayor que la media de las fincas tratadas)}\]
6.4.4 Dos colas
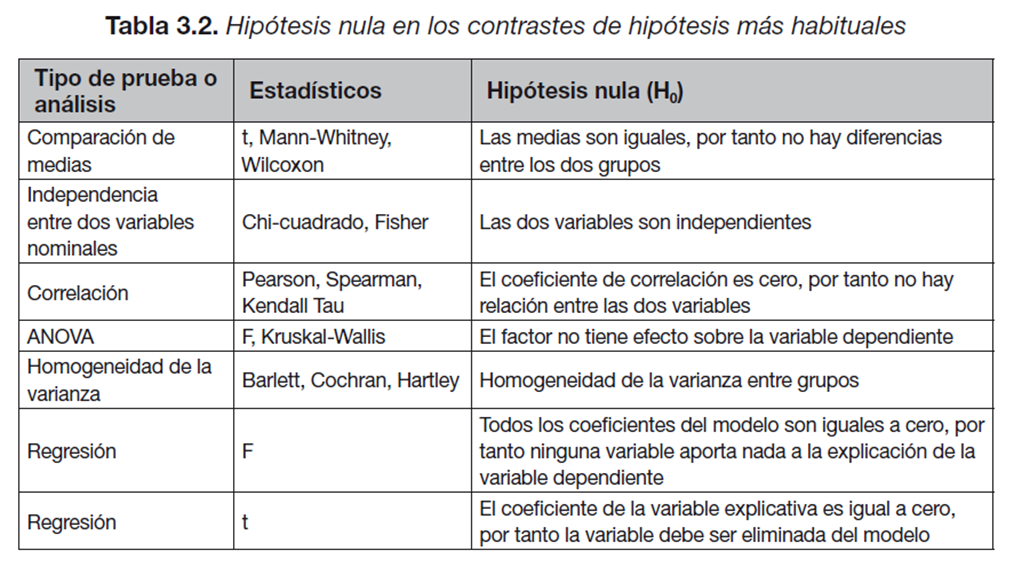
Tenemos una prueba de dos colas cuando la prueba de hipótesis queda expresada como el siguiente ejemplo: \[H_0: \mu_A = \mu_B \text{ <--- (no existen diferencias entre las dos medias)}\] \[H_0: \mu_A \neq \mu_B \text{ <--- (las medias de las fincas tratadas con A o B son distintas)}\] ¿Qué implica el hecho de considerar una prueba con una o dos colas? < br> En el primer caso, una cola, el valor crítico que determina rechazar o no la hipótesis nula deja a la derecha la totalidad del nivel de significancia (\(\alpha\)). En el caso de una prueba de dos colas, este vlaor deja a la derecha (o a la izquierda para un valor negativo) la mitad de esta probabilidad (\(\alpha/2\)). Esto implica que en una prueba de dos colas es más difícil rechazar la hipótesis nula ya que el valor crítico es mayor. Por ejemplo, en una distribución normal el valor crítico que deja el 5% de la probabilidad a la derecha es igual a 1.65, sin embargo este valor aumenta hasta 1.96 con sólo el 2.5% de la superficie a la derecha.
A continuación una imagen que ejemplifica éste concepto: